In the previous post I looked at the main factors other than internal air temperature that affect how thermally comfortable we feel in a room. Internal surface temperature played a big role, both because of its influence on radiant heat loss and because of the ability of cold surfaces to cause fast-moving air through down draughts.
In this post I’m going to look at typical internal surface temperatures for different standards of construction. I summarise the key points in the main post, and those of you that are interested in how the figures are calculated can read on.
Building elements (walls, windows, doors, roofs and floors) that are poorly insulated will have a lower internal surface temperature when it is cold outside than elements that are well insulated. The degree of insulation is given by the U value, poorly insulated elements have a high U value, well insulated ones have a low U value. The table below looks at surface temperatures we could expect in different building elements in a hypothetical winter situation where it is 0°C outside and 20°C inside.
| Building element | U value | Internal surface temperature when internal temperature is 20 °C and external temperature is 0 °C |
| Single glazed window | 5.778 W/m2K | 5°C |
| Double glazed window, air fill, no special coatings on glass | 1.960 W/m2K | 14.9°C |
| Passivhaus standard triple-glazed window | 0.6 W/m2K | 18.4°C |
| Solid brick, uninsulated wall | 2.062 W/m2K | 14.6°C |
| Typical new build wall | 0.2 W/m2K | 19.5°C |
| Typical Passivhaus wall | 0.1 W/m2K | 19.74°C |
| Uninsulated concrete lintel (thermal bridge) | 2.929 W/m2K | 12.4°C |
As you can see, the internal surface temperatures of some of the elements you might get in an old home are extremely low. Surface temperatures of 5°C for windows will make the area around a window feel especially chilly due to radiant heat loss, and also cause internal air movement due to down-draughts. Even walls, in old houses, can have surface temperatures that are low enough that they add substantially to radiant heat loss and air movement.
Thermal bridges, caused by either poor design or poor construction, although they typically cover quite small areas, can have a significant impact on internal surface temperatures. Note that if the lintel or thermal bridge were steel rather than concrete the impact would be much higher still, since steel is around 100 times more conductive than concrete.
How does this make me feel?
Thermal comfort models are quite complex, but a simplified method for estimating how warm a room ‘feels’ is simply to take an average of the air temperature and the mean internal surface temperature. My house, when it is 0°C outside and 20°C inside, with surface temperatures for (double glazed) windows of 14.9°C and (uninsulated) external walls of 14.6, feels like an isothermal (surface temperatures the same as air temperatures) house with an air temperature of 17.4°C. Compare this with a Passivehouse standard building which, in the same conditions, would feel like an isothermal house with an air temperature of 19.5°C. So for the same weather conditions and the same internal air temperatures, a house built (or retrofitted) to Passivehouse standards feels over 2°C warmer. This is remarkable, especially given that it doesn’t include the effects of air movement and external draughts which will also be considerably improved in a Passivehouse building.
Summary
Building, or retrofitting, to very low energy standards raises internal surface temperatures in cold weather dramatically, and this makes them feel more comfortable both because of reduced radiant heat loss and reduced air movement. Passivehouse standard requires that surface temperatures never drop more than 4°C below the air temperature, in addition to a host of other comfort requirements.
How do we calculate these temperatures?
The rate at which heat flows through different building elements (walls, windows, doors, roofs and floors) is dependent on the how well insulated they are and the difference in temperature between inside and outside. How well insulated they are is measured by the U value, which gives the rate of heat flow in watts, per square metre of building element for every degree Celsius difference in temperature between inside and outside. The units for U value are W/m2K1. If it is the same temperature inside and outside then no heat flow takes place. The bigger the temperature difference and the higher the U value the larger the rate of heat flow. So if a wall has a U value of 1 W/m2K and it is 0°C degrees outside and 20°C inside then the heat flowing through a m2 of that wall will be 20 W. The better insulated the building element the lower the U value and the lower the heat flow for a given temperature difference.
The U value of a building element with multiple layers (such as a wall) is determined by the thermal resistance of each layer. If we know the U value, and the internal and external temperatures, then we can calculate the heat flow through the building element (as I did above). And if we know the proportion of the total thermal resistance that each layer contributes then we can calculate the temperature at different points in the structure. Thermal resistance is given in units of m2K/W, this is the reciprocal of the U value.
The first layer with thermal resistance is the thin layer of air sitting next to the element on the inside surface. This is called the surface internal resistance. In a well insulated element the effect of the surface internal resistance is minimal (because it provides much less resistance than the insulation), but knowing its value is still very useful – we can use it to calculate internal surface temperatures.
The higher the thermal resistance of a material the bigger the drop in temperature from one side of a material to the other. Think of a tea pot – the temperature of the water inside the pot is close to boiling and the surface temperature is very hot, too hot to hold, because the pottery the tea pot is made of has low thermal resistance. Put the same close-to-boiling water in a thermos flask and you can hold it comfortably, in fact the heat flow through the flask is so low you can hardly feel it at all. The thermos has a much higher thermal resistance and so the temperature drop across the material much higher. So how does this work in buildings, and how can we use it to calculate internal surface resistance?
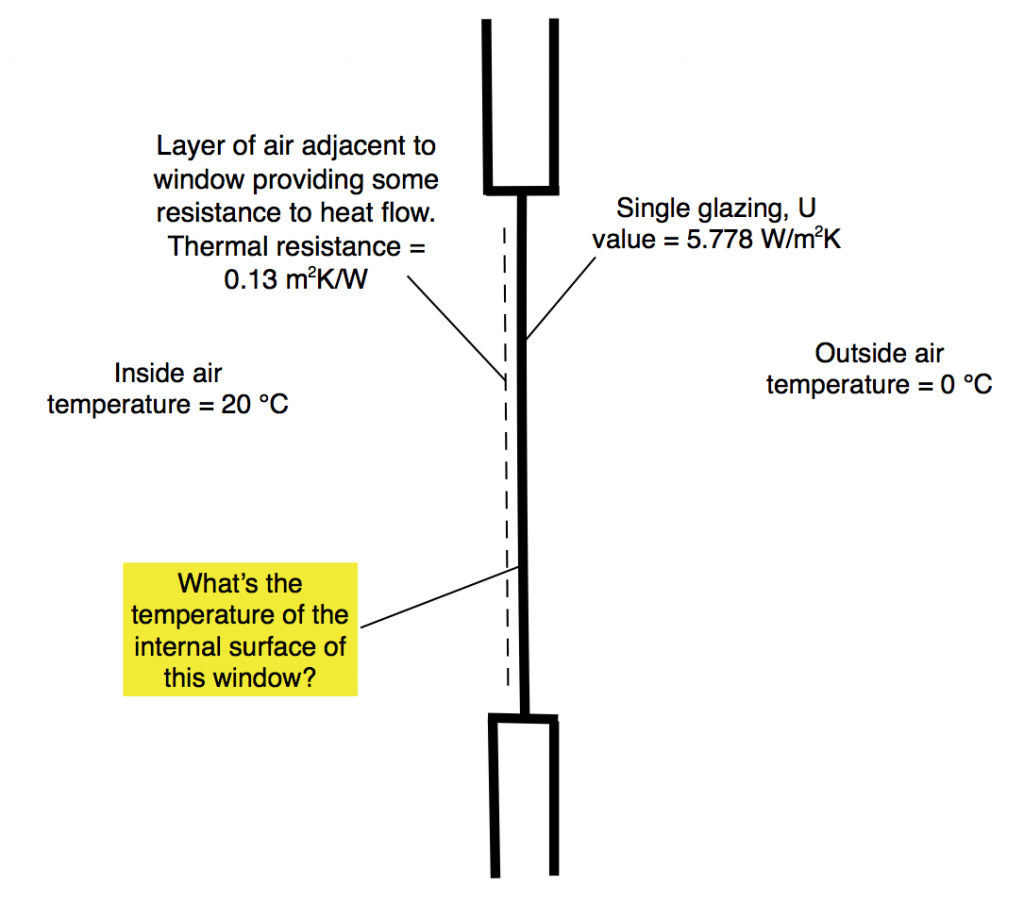
Let’s start with an extreme example, the single glazed window shown above. Glass is a poor insulator so the surface resistance is much more significant proportion of total thermal resistance than it would be for a typical wall.
The glazing U value for a single glazed window is 5.778 W/m2K, this value includes the effect of internal surface resistance. If it is 0°C outside and 20°C inside then the heat flow is
5.778 * 20 = 115 W for every m2 of glazing.
Internal surface resistance for a vertical surface is 0.13 m2K/W. The temperature drop from one side of a resistive layer to the other (in this case the layer of air on the inside surface of the window) is equal to the heat flow multiplied by the resistance.
115 W/m2 x 0.13 m2K/W = 15 K or 15°C
So if the internal temperature is 20°C and the external is 0°C, the surface temperature of a single glazed window would be 5°C. The same calculation was used to get the surface temperatures for different elements in the table above.
